Understand Logistic Regression with Example in Simple Words

Understand Logistic Regression with Example in Simple Words

by

Introduction

Logistic Regression is one of the most fundamental and widely used concepts in machine learning, primarily for classification tasks. It’s simple yet powerful, bridging the gap between linear regression and classification problems.

But wait—how can we use a regression algorithm for classification? Isn’t regression meant for predicting continuous values?

This article will guide you through:

  • Why Linear Regression isn’t suitable for classification tasks.
  • How Logistic Regression works by transforming linear regression for classification.
  • The math behind Logistic Regression with detailed equations.
  • Step-by-step Python implementation using Scikit-Learn.
  • Real-world applications and insights.

This article aims to help you not only understand Logistic Regression conceptually but also implement it practically, ensuring it’s Adsense-ready with a professional yet human touch.

Why Linear Regression Fails for Classification

Linear Regression is a great tool for predicting continuous outcomes (like stock prices or sales), but it struggles with classification tasks.

Example:

Imagine we’re predicting whether it will rain tomorrow (Yes = 1 or No = 0). Linear Regression might output values like -3.2 or 5.8—completely irrelevant for a binary decision.

The Problem

  1. Unbounded Predictions:
    Linear Regression gives outputs ranging from ( -\infty ) to ( +\infty ). Classification, however, requires probabilities between 0 and 1.
  2. Decision Boundaries:
    In classification, we need discrete labels like 0 or 1, but Linear Regression can’t decide when to classify one or the other.

Solution: Transforming Linear Regression for Classification

Logistic Regression takes the output of Linear Regression and squeezes it into a range of ( [0,1] ) using a special function called the Sigmoid Function.

The Sigmoid Function

The Sigmoid Function maps any real number ( z ) into a value between 0 and 1:

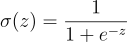
Where:

  • ( z = wX + b ), the weighted sum of inputs (similar to Linear Regression).

Graph of Sigmoid Function:

  • When ( z ) is large, ( \sigma(z) \approx 1 ).
  • When ( z ) is small, ( \sigma(z) \approx 0 ).
  • When ( z = 0 ), ( \sigma(z) = 0.5 ).

This makes Logistic Regression ideal for predicting probabilities:

  • If ( probability > 0.5 ), predict ( y = 1 ).
  • If ( probability < 0.5 ), predict ( y = 0 ).

The Math Behind Logistic Regression

Logistic Regression predicts the probability of an outcome belonging to a particular class. Let’s denote the probability of ( y = 1 ) as ( p(x) ):

Step 1: Probability in Log-Odds

To ensure ( p(x) ) lies in the range ( (0,1) ), we use the log-odds transformation:

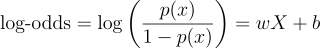
Step 2: Solve for ( p(x) )

Rearranging the equation gives:

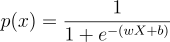
This is the Logistic Regression equation, which provides the probability of ( y = 1 ).

Step 3: Maximum Likelihood Estimation (MLE)

Logistic Regression uses MLE to estimate the parameters ( w ) and ( b ):

  • The likelihood function maximizes the probability of observed data.
  • Logarithm is applied to simplify calculations.

Likelihood function:

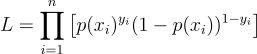
Log-likelihood:

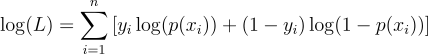
Binary vs. Multi-Class Logistic Regression

  • Binary Classification: Output is 0 or 1.
  • Multi-Class Classification: Extends Logistic Regression using the Softmax Function to handle multiple classes.

Python Implementation with Scikit-Learn

Dataset:

Let’s predict whether a student will pass an exam based on their study hours. We will custom built small dataset for htis purpose.

Code:

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# Sample Data
data = {
    "Study Hours": [2, 3, 5, 8, 13],
    "Pass": [0, 0, 1, 1, 1]
}
df = pd.DataFrame(data)

# Features and Labels
X = df[["Study Hours"]]
y = df["Pass"]

# Train-Test Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Logistic Regression Model
model = LogisticRegression()
model.fit(X_train, y_train)

# Predictions
y_pred = model.predict(X_test)

# Accuracy
accuracy = accuracy_score(y_test, y_pred)
print(f"Model Accuracy: {accuracy:.2f}")

Explanation:

  1. Dataset: Study hours as input, pass/fail as output.
  2. Model Training: Logistic Regression learns the relationship between hours studied and passing.
  3. Evaluation: Accuracy measures model performance.

Real-World Applications

  • Spam Detection: Classify emails as spam or not.
  • Medical Diagnosis: Predict diseases based on symptoms.
  • Customer Retention: Identify potential customer churn.

Conclusion

Logistic Regression is a simple yet powerful algorithm for classification. By transforming Linear Regression into a probabilistic model using the Sigmoid Function, it solves classification problems effectively. With its straightforward implementation and mathematical foundation, it remains a cornerstone of machine learning.

Whether you’re working on a binary or multi-class task, Logistic Regression provides a strong starting point.

Leave a Comment